Thinking about intelligence

Investigating my intuitions

Motivated by the mysterious nature of human reasoning, during 2019, I found the time to start exploring the world of artificial intelligence, choosing though a rather unconventional approach. Instead of digging right into machine and deep learning courses, and start playing with TensorFlow and PyTorch, I decided to start by developing a framework that explains my own intuitions about the brain and work my way from there. Once I had the basic principles and a proper structure of such a framework in place, I would compare it with the established knowledge to see how close or how far I am. No matter if the outcome would be completely wrong or not, I knew that it is always much easier to understand the fundamentals if you have first tried to explain them by yourself. During this period and as some things were starting to crystallized, I kind of cheated. I started watching talks of three of the most influential people of modern AI, Geoffrey Hinton, Yoshua Bengio and Yann LeCun, so my thought process has been influenced by them. (It would be unfair though not to mention Jeff Hawkins and his HTM theory. He is not considered mainstream but I gained a lot of useful insights from his talks too). Some things made perfect sense to me, others were completely new and some others are yet beyond my comprehension. As I discovered in the process though, my thinking led to a self supervised learning model that uses autoencoders (among other things).

Note: In the rest of this post I try to describe the thought process that led to some of my initial conclusions. They might contain inaccuracies or errors, so if you are new to the field, have in mind that you could be misguided by them. If you are experienced on the other hand, try not to be too strict on them. They are just the untested ideas of a curious person who explores his intuitions. Until they are verified or discarded by actual implementations and testing, they remain ideas that might be useful just as some short of inspiration. In matter of fact I believe that some of these concepts are really promising and might lead to interesting paths, so I have every intention to test them by myself, once I find the time to do so. In any case I will keep this post updated. Take what you read with a grain of salt.

Concepts correlation

My main intuitions come from observing my own brain and the way I reason about things. One very obvious phenomenon that caught my attention and was the starting point of my journey, is what I called concepts correlation. A typical example of this phenomenon is this: When we hear dog barking, a visual representation of a dog can be generated “in our mind”. A lot of other things can be generated too but let’s focus on the correlation between the auditory and visual signals at the moment. The opposite is also true. If we see a muted video of a barking dog, we can imagine the barking sound, or in other words, the barking sound is generated by the sight of a barking dog. How this correlation between the two signals is achieved? This is what I initially wanted to understand. I wanted to understand the mechanism with which two sensory inputs are correlated with each other, in a way that when one of them is activated, it generates a representation of the other. We can even go one step further and replace the barking sound with the sound of the word “dog”. Fundamentally, they are both two simple auditory signals. The word dog is just a specific sound that is related with an object, in this case the dog and the mechanism that relates them could be identical with the one that relates the barking sound with the sight of the dog.

Encoders

The way I approached this issue was by thinking in terms of neural networks that process the seemingly random input signals and produce simple compact representations of the main patterns find in them.

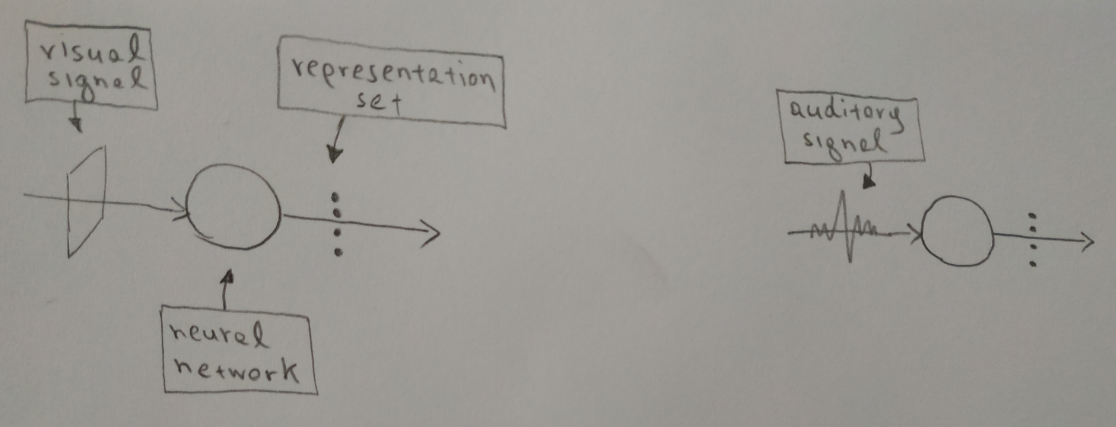
A typical multi layer neural network is composed by many layers of neurons, each one of which process the output of the previous layer. Usually the input layer has far more neurons than the output layer. This way the input layer can represent signals that contain a lot of details (high-dimensional signals) while the output layer can only represent “rough” signals with not much detail (low-dimensional signals). We say that a neural network learns to identify a pattern in the input signal, when it produces the same output every time it receives signals that contain this pattern. Let’s not focus on what drives this learning process, let’s focus on the result. An input signal represented by a large number of firing neurons in the input layer, is transformed to a small set of of firing neurons in the output layer. This set of firing neurons of the output layer, represents a pattern of the input signal, or using a more generic term, it represents a “concept”. For this reason I call this set of firing neurons, the representation set of this concept. Every distinct sound and every distinct object corresponds to an input signal which is processed by a neural network and is eventually represented by a specific representation set in the output neurons of the network. Through this prism, every time we see a dog, the same representation set is activated. This representation set can be thought of as an encoding of the semantics of the input signal or a compressed representation of it, so the neural network that creates it can be called Encoder.

This basic process can be easily depicted with a very simple diagram that also shows the notation I use.

Note: The transformation of an input signal to an output one, performed by a neural network, can be thought of as the transformation of a vector between an input and an output space where the input space has more dimensions from the output space. The output space is usually called latent space.

In the context of the previous example, when we see a dog, the visual field which is a collection of colors and shapes is transformed to an electrical signal, is processed by the visual system and is narrowed down to a specific set of firing neurons that collectively, they represent the pattern of a dog and can be called the dog’s representation set or dog’s latent vector. (Let’s not focus on what type of neural networks are good for visual signal processing nor the exact methods they do it). The same process takes place in the auditory system too. The word “dog” which fundamentally is a sequence of air vibrations, is transformed to an electrical signal, processed by the auditory system and narrowed down to a specific set of firing neurons that represent the pattern of the word “dog”. If this is the case, then how these two representation sets (or latent vectors) are correlated with each other so that one can be generated by the other?

Correlators

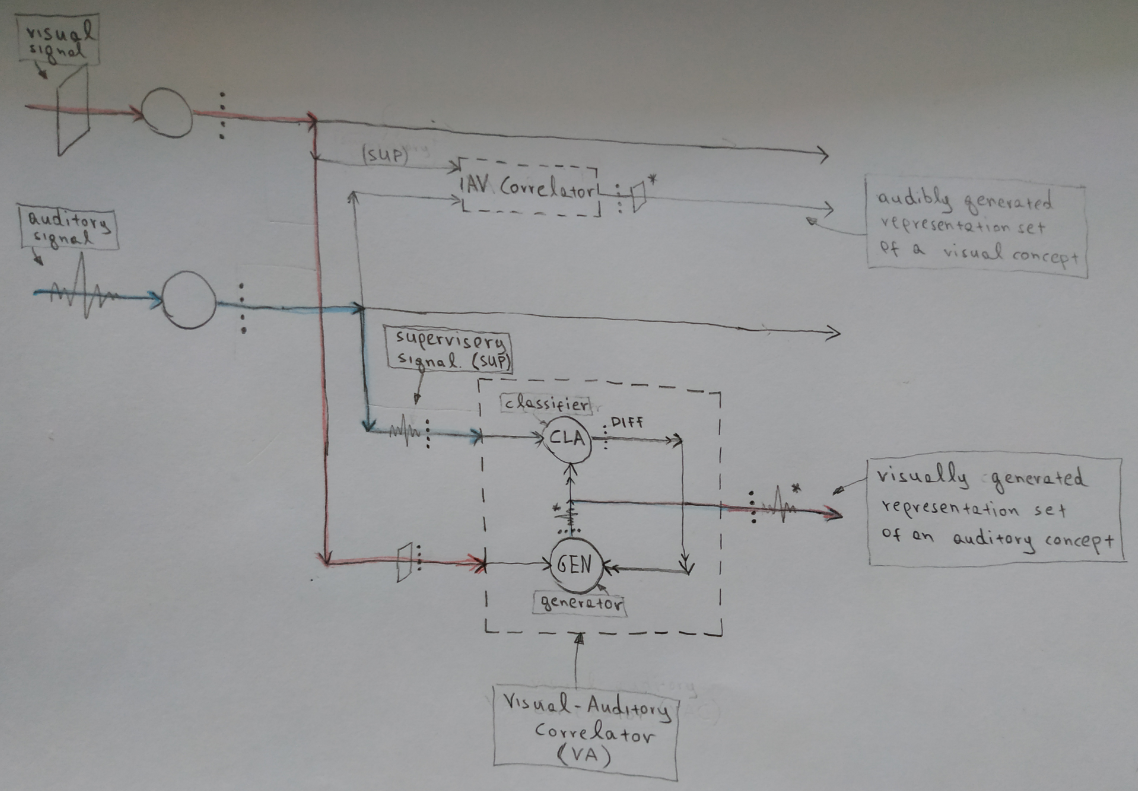
Another obvious phenomenon is that in order for two “concepts” (representation sets or latent vectors) to be correlated with each other, they must be active at the same time. For example when we stand next to a barking dog, the sight of the dog and the sound of the barking are processed simultaneously and both representation sets are active at the same time. Similarly when we learn the word “dog” the visual and auditory signals must be received at the same time in order to learn that the word “dog” refers to the dog. During that time a training process that correlates the two representation sets must take place. The training must be done in such a way, that the representation set generated by a signal of sensory modality A (vision), is used to generate an approximation of the representation set of a correlated signal of sensory modality B (hearing). Approximation in this context means, that this generated representation set should be classified to the same class with the representation set of the actual correlated signal of sensory modality B. Such a mechanism is described in the following diagram.

There are two sensory modalities involved. Vision and hearing. Two representation sets are created, one for each sensor. The two representation sets are the input to a system named Correlator. One of the two sets has the role of the supervisory signal and the other of the seed signal. The seed signal must generate a representation set that approximates the supervisory signal. The Correlator has two units (neural networks), a Generator and a Classifier. The generator receives the seed signal and generates a representation set that tries to match the supervisory set. The generated set is received by the classifier which also receives the actual supervisory set and outputs a correction or “difference” signal. This signal tries to modify the generator so that it generates a set that is classified at the same class with the supervisory set. This is the training of the system. After a certain training period the generator will output a set that approximates the supervisory set. The generator’s output, is also the correlator’s output.

Note: This is just one of the possible architectures of a correlation mechanism. There might be alternative architectures that achieve the same result in a different way. What’s important is to achieve the goal of correlating two representation sets with each other in a way that when one of them is activated, it generates a representation of the other.

When the seed signal is the visual representation set and the supervisory signal is the auditory representation set, what is output from the correlator is a visually generated representation set of an auditory concept. In the context of the dog example, this output is the “internal sound” of the word “dog” which is generated “in our mind” when we see a dog, or the barking “sound” when we see a muted video of a barking dog. The two sensory representation sets must be active together for a sufficient amount of time for the correlator’s training to take place. There is also a second identical correlator to which, the seed and supervisory signals are the other way around. Eventually, this correlator will receive the representation set of the word “dog” and will generate a representation of the image of a dog, or more formally it will output an audibly generated representation set of a visual concept.

What’s important to remember, is that according to this model the correlation is achieved in the latent space, at representation set level, between low-dimensional high-level concepts.

Some notes

• The latent space must be low dimensional enough so that the latent vectors are simple to facilitate the processes that work with them (like the correlation process). They must also be rich enough so that they contain the fundamental semantics of the input space and so that their correlated vectors can be generated by them.
• In this model, the training of the sensory units is independent of the correlators training. The correction signal is only received by the generator. In an alternative scenario, the correction signal produced by the classifier, apart from the generator’s training might contribute to the sensory units training too. This might be necessary so that they produce slightly different representation sets that are easier to correlate. Although, intuitively I would say that this is not the case. Imagine that you have seen many dogs and have learned to recognize them, but you have never stand next to a barking dog. You have heard barking many times but you have no idea that its a dog’s voice. At this point the representation sets are well established but not correlated. If you finally see and hear a dog barking I think that you would easily correlate the two without much effort. By correlation I mean that you could imagine a dog by hearing barking and vice versa. So, I would argue that in this scenario the training is only applied to the correlator and not to the sensory units that produce the two representation sets.
• The classifier’s correction signal is like a loss function. There might be different types of classifiers.

Decoders

The Decoder is a unit that does the opposite job of the encoder. It transforms from the latent space to the input space. It receives a representation set and generates an approximation of the input signal that created this representation set in the first place. The input to a decoder can be either the representation set produced directly by the encoder or its approximation, the representation set produced by the correlator. The following diagram is an enriched version of the correlators’ diagram which contains the decoders too.

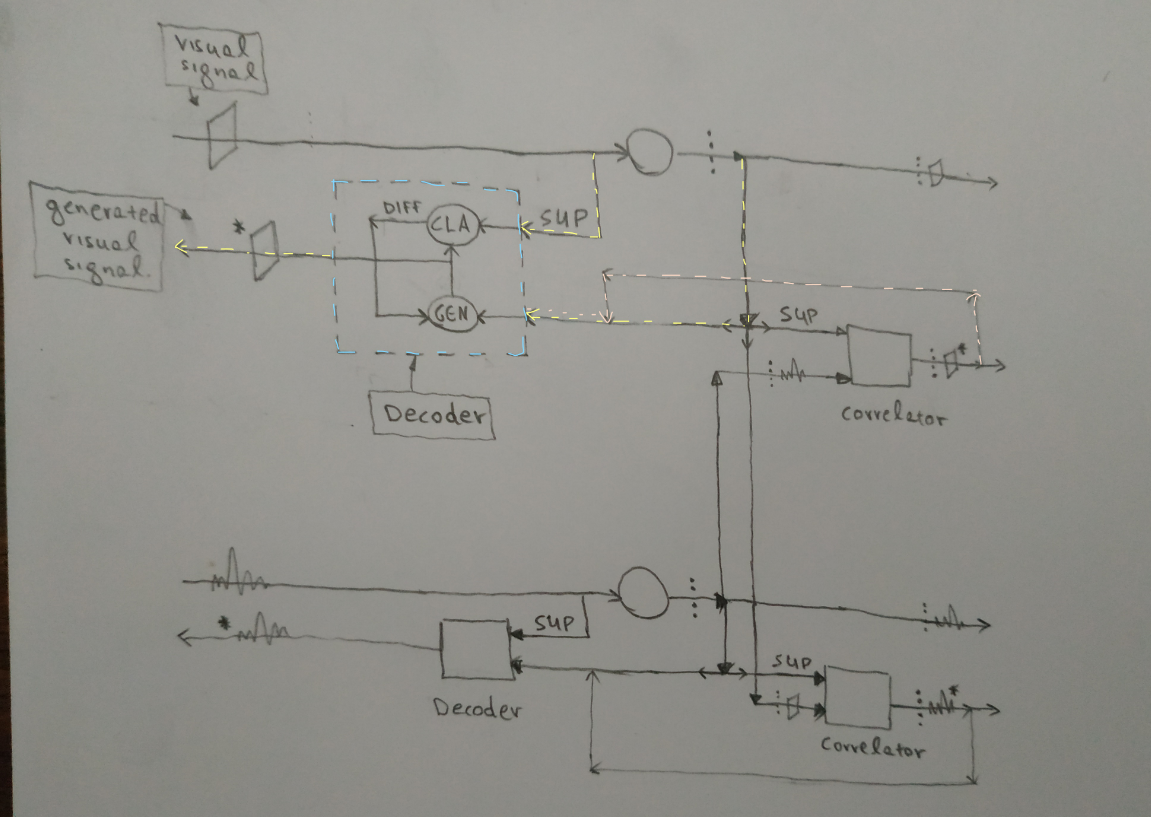
In this model, the decoder contains a generator and a classifier, similarly to the correlator, so its training is very similar too. The high-dimensional vector is the supervisory signal while the low dimensional latent vector is the seed signal. The generator tries to generate an approximation of the high dimensional signal by processing the lower-dimensional signal. The classifier generates a correction signal that trains the generator.

The fact that the correlator’s output is connected to the decoder is very important. When there are two correlated signals, one of them, the seed, can generate an approximation of the other’s representation set. This set, which is an approximation of the supervisory set, can be decoded back to the supervisory signal in the input space. So, the seed signal can generate the lower level supervisory signal and vice versa. For example, auditory signals can generate lower level visual signals. This means that when we hear the word “rectangle”, it is encoded to a representation set which is the seed that creates the representation set of a visual rectangle, which can be decoded back to the lower level visual input signal of a rectangle.

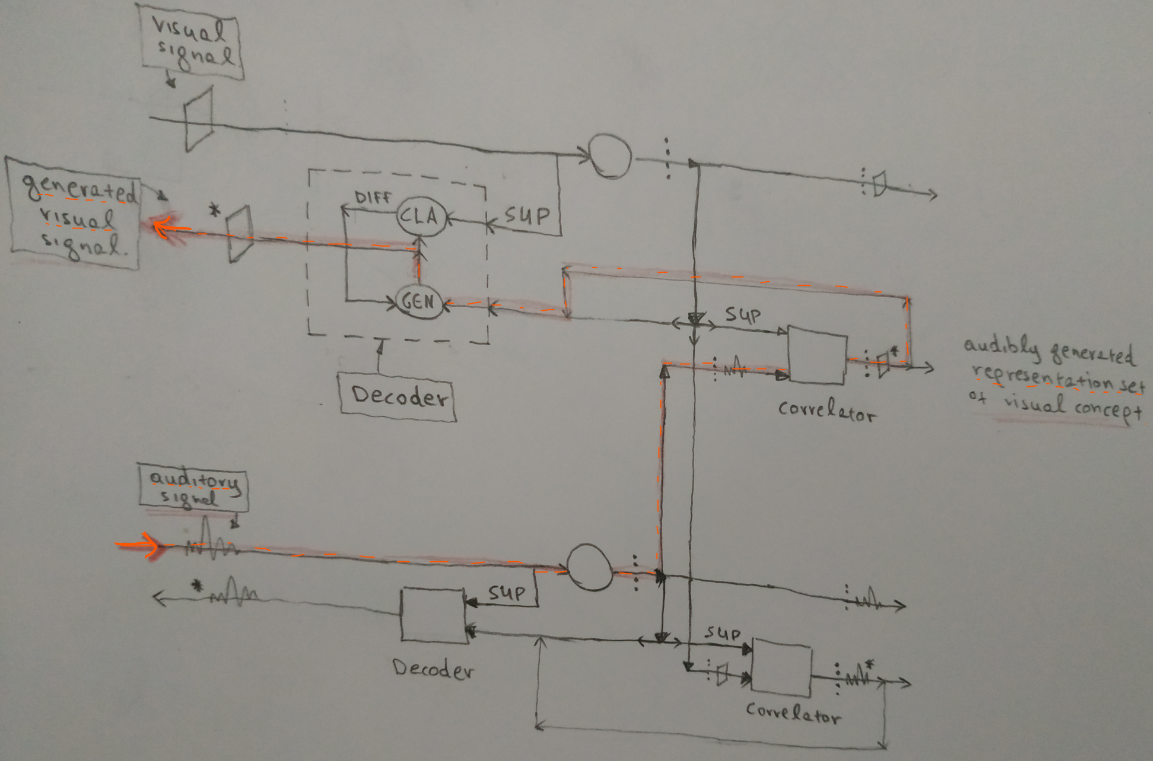
Note: The lower level supervisory signal can be further decomposed to even lower level signals. Decoders have a crucial role in the structure of a hierarchical system.

Hierarchies

One of the reasons that deep neural networks are good at processing sensory signals (say pictures, which are snapshots of the real world), is the fact that the input data is compositional. A rectangle for example is composed of lower level patterns, the lines and the corners. Similarly every object is composed of simpler lower level patterns and these patterns of even simpler ones and so on. This compositionality exist for all sensors. The world data is inherently compositional, so any sensor that process it, will receive compositional signals.

This compositionality can be mirrored to the structure of a hierarchical system that processes compositional data. Such a hierarchical system can be structured using encoders, correlators and decoders as they are previously defined. First, let’s see a diagram, without correlators, that describes the basic composition and decomposition process.

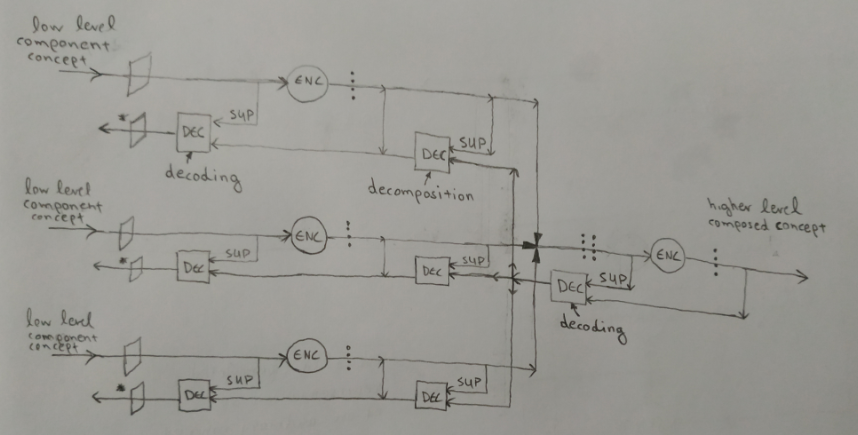
There are three simultaneous input signals that are processed and recognized, meaning that a representation set is activated for each one of them. The three representation sets, that are active at the same time, can be thought of as a single unified signal, a composed signal or composed representation set, which is the input to an encoder in the next level, that process it and encodes it to a higher level representation set. This set is an encoded version of the composed representation set and represents a high concept which is composed of the lower level component concepts that were activated simultaneously at a previous level. As an example, if the higher composed concept is a rectangle, the lower level components could be lines and corners.

The opposite process can also be achieved. If the composed concept is activated first (for example by a correlated high concept), then its components can be generated from it with the use of decoders. Initially the composed representation set is decoded to the composed signal which is an approximation of the combined lower representation sets. This signal is decomposed to the individual representation sets that compose it, with one “decomposer” per component. This process can be called decomposition, as opposed to decoding (which inverts the encoder’s process). Then each individual representation set is decoded back to an approximation of the component’s input signal.

Correlation trees

Apart from being convenient for processing compositional data, a hierarchical system constructed by distinct basic components, is also a mechanism that can be used to construct an associative thought process. Since each component is a distinct representation set, a distinct concept, it can be correlated with others not only to generate higher composed concepts, but to generate a chain of activation of correlated representation sets. For example a specific smell, might remind a specific place, that might remind a specific face, that might remind a specific feeling (associative memory). The smell’s representation set has been correlated with the place’s representation set, which has been correlated with the face’s representation set, which has been correlated with the feeling’s representation set. This propagation of activations of correlated representation sets, is a correlation chain. As this chain evolves, each individual representation set could be decomposed to its components through its hierarchical structure. An example can be shown in the following diagram. It adds the correlators into the mix.

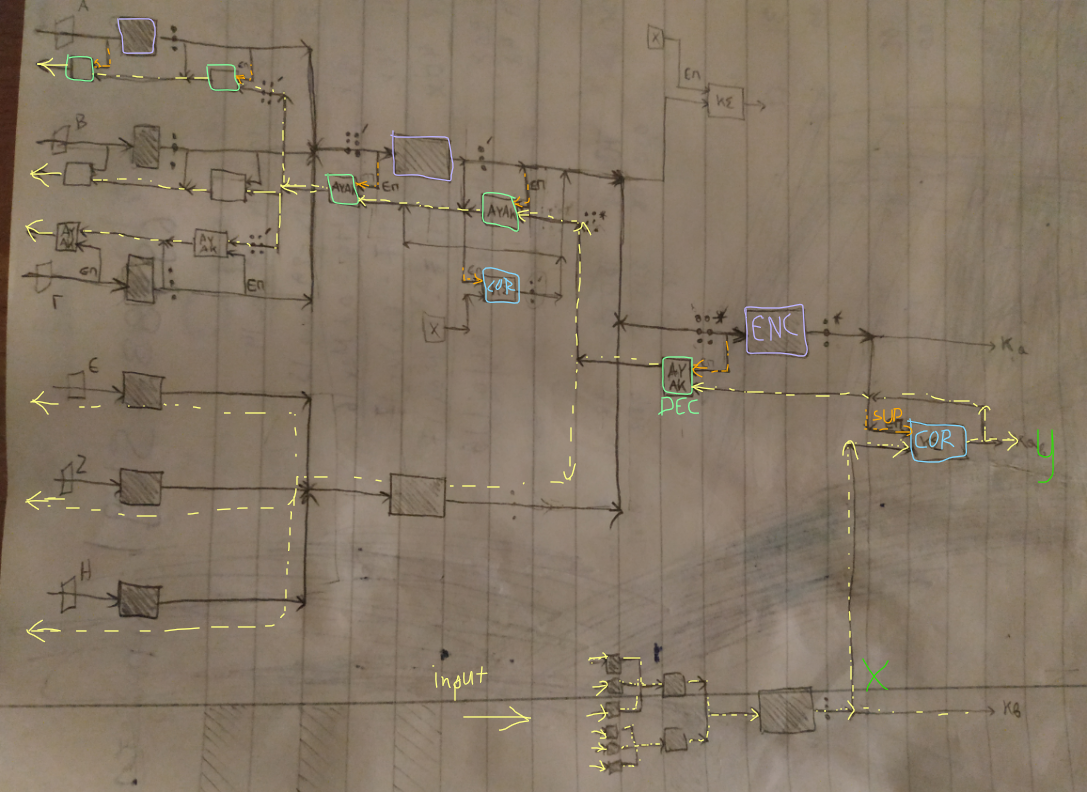
The diagram indicatively contains two correlators only, but you can imagine that each component’s representation set can have at least one correlator that correlates it with another representation set. In the diagram, an input signal is encoded to components that compose the higher representation set x, which activates the correlated representation set y (through a correlator) and this correlated set is decomposed to its own components. Representation set y can also activate its own correlated sets and those theirs and so on, in a chain that is not shown in this diagram. The lower level components could also be correlated with other representation sets and these with others. This propagation structure is the correlation chain, of which, two links (the two correlated representations sets x and y) are shown in this diagram.

Note: Since a representation set can be correlated with more than one other sets, the correlation chain can form a tree of activity, with many branches. For this reason the term correlation tree as a more generic one, is probably more appropriate.

Reconstruction chains

The reconstruction chains is an idea that arose during the investigation of the correlation chains. It’s something that adds a few nice properties to the system, but as anything that is untested and with no references, might be just a nonsense. In any case the rest of this exploration doesn’t require their existence.

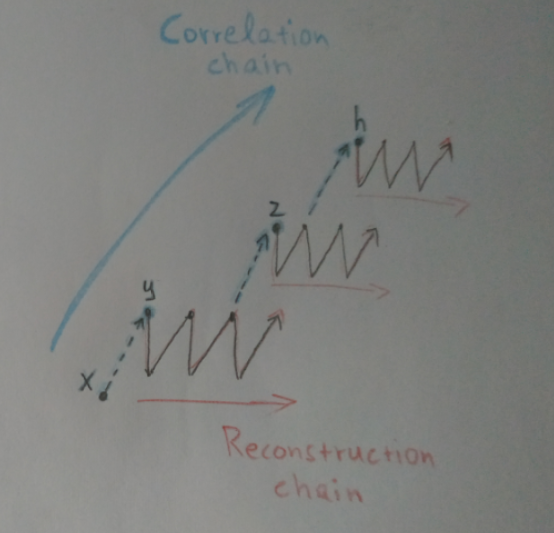
Having said that, let’s see what is it about. A reconstruction chain is a series of composition and decomposition cycles of a representation set’s hierarchy. The previous diagram which describes in detail two links of a correlation chain, the correlated sets x and y can be further simplified with the following diagram. A representation set x activates its correlated representation set y which is decomposed to its components. These components are the input to another hierarchical system that process them and regenerates a new instance y’ of the composed representation set y. This instance is decomposed to its components too and these regenerate yet another instance, y”. This cycle of compositions and decompositions can propagate further until it eventually stops at the end of the underlying connectivity.

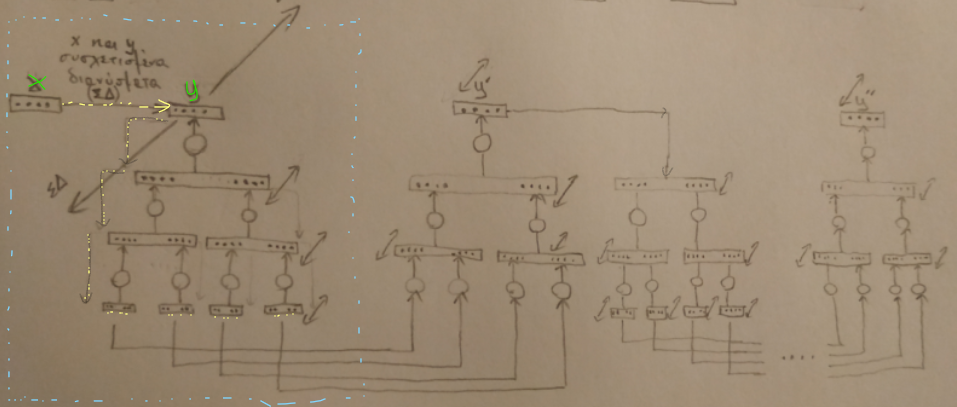
Reconstruction chains offers some important properties to a system that uses them. Diversity and redundancy. Every instance of a specific representation set, is based on different underlying “hardware”, but represents the same concept. This means that this concept, through its many instances, lives for a larger period of time and it propagates to different areas of the system too, increasing the probability of correlation with other propagating concepts. According to my thinking, concepts correlation is one of the fundamental mechanisms of reasoning so anything that facilitates it must be important. Another aspect is that it makes the system resilient to hardware damage since a concept can be generated in more than one places within the system (either through input signals or through its correlations). Of course there might be other alternative mechanisms that can achieve these properties. Reconstruction chains is just one approach. If we represent a reconstruction chain by this simple diagram:

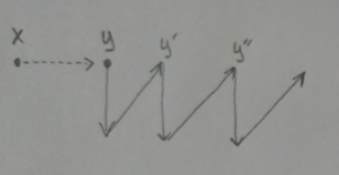
Then using this notation a correlation tree along with its reconstruction chains, can be represented by the following diagram:

Active State

A system that processes continuous sensory inputs, correlates concepts, decomposes them and generates new ones in a continuous flow, must be teeming with activity. If we try to think about it in terms of the previously defined framework (representation sets, correlations, chains) then this activity is a collection of correlation trees and can be referred to as the current active state of the system. This state is dynamic. It is continuously modified either by sensory signals or by the propagation of correlating concepts.

If we accept that the internal activity of individual computational nodes (encoders, decoders, generators, classifiers) doesn’t play an important role in reasoning, but only the outcome of their processing which is the representation sets, then we can think of the active state as a collection of representation sets of high-level concepts.

Note: It is interesting to contemplate that any new thought, which is itself represented by certain representation sets, must be generated by the current active state.

Selection system

In order to avoid the chaos which might arise from a huge number of simultaneous active concepts propagating their chains and decomposing their concepts all over the active state, it seems reasonable to think that there must be some kind of mechanism that selects which of the current active concepts to focus the “attention” of the system to. But what focusing means in this context? One aspect of it could be selecting which ones will propagate further and/or which ones will be decomposed. But how something can allow or deny the further propagation of specific branches of a correlation tree or the decomposition of its concepts? One idea is a switch mechanism. According to this idea, there is a correlation switch in the connections between two correlated concepts and a decoding switch in the connections between the components of a hierarchy. The first type controls the propagation of the correlations while the second one the decomposition to components. There can be various implementations of such a switch mechanism. One approach is with a bypass to an external “selection system” (or attention system). The connections are routed to this system which “decides” (in a reward based process) if it will send back the received signal or not. By “blocking” the incoming signal it stops the propagation of correlations or the decomposition process.

Essentially such a mechanism selects which of the active concepts are currently important and which aren’t, by choosing which ones to propagate and/or which ones to decompose, influencing the evolution of the active state. Important concepts will propagate and analyzed, while the rest of them will fade out. This mechanism requires an external system to which all representation sets have connections with, and it has connections back to each one of them too. In this context the representation sets of the active state can be thought of as seeds from which the selected ones will generate new representation sets that will become seeds themselves.

This system needs to gradually learn which concepts and combinations of concepts to allow and which to suppress, at any point in time. This is where a reward system might be necessary. Whenever the system pays attention to the “right” things, there is a reward that reinforces its current settings. What things are the right things in each situation is a big issue and the reward mechanism is of great importance for such a system.

Further exploration

There is so much room for exploration in all of the concepts described in this post. There is also a group of fundamental issues which I haven’t explored yet much, things like the reward mechanism and how is related with the concept of prediction, or how language and motion are generated by sequence processors that are fed with selected representation sets from the active state. And eventually how all these concepts can be combined to an autonomous agent which can interact with the environment and learn from it. What a luring challenge.

I have to emphasize once again, that many of the things described in this post just come from my imagination and are yet completely untested. They are the result of an effort to try to understand and explain, through the use of neural networks, some fundamental phenomena that I observe in the function of the brain. The initial conclusions from this raw thought process might be useful as inspiration but might be misguiding too. Retrospectively though, I can say that some things are in the right direction, for example encoders and decoders are fundamental parts of autoencoders a well established type of neural network, the existence of which I didn’t know when I started. Another fundamental concept that points to the right direction is self-supervised learning, a process in which the system doesn’t need existing labeled data as supervision but uses it’s own observations instead. The requirement for a reward system which seems to be fundamental in humans is also important or the relationship between words and representation sets that represent concepts of the environment. I have yet though no idea about how difficult would be to train a system that combines so many networks with each other or how such a system would perform.

We must also have in mind that there is a trap when we try to mimic the behaviour of biological systems. This trap can become obvious with the famous birds and planes example. You can understand the basic principles of flight by studying birds, but once you understand them you can create artificial implementations that aren’t exact copies of the biological source. So, planes fly without flapping their wings. Trying to create planes that fly exactly the way birds do, would be far more difficult and ultimately unnecessary. In an analogy, if the fundamental principles of reasoning are understood, the actual implementation of the system might have significant differences with the human brain.